?2023年內蒙古專升本高等數學Ⅱ考試大綱

2023年內蒙古專升本高等數學Ⅱ考試大綱

普通高校專升本考試(以下簡稱“專升本考試”) 是普通高 校全日制高職應屆畢業生升入普通高校全日制本科的選拔性考 試，其目的是科學、公平、有效地測試考生在高職階段相關專業 知識、基本理論與方法的掌握水平和分析問題、解決問題的能力， 以利于各普通本科院校擇優選拔， 確保招生質量。專升本考試貫 徹黨的教育方針， 落實立德樹人根本任務，促進高素質技術技能 人才成長， 培養德智體美勞全面發展的社會主義建設者和接班人。

《高等數學 Ⅱ》作為專升本考試理工類 2 的專業基礎課，其 考試說明依據自治區高職院校高等數學課程標準以及本科高等 數學課程教學要求，結合自治區實際制定。注重考查考生對所學 高等數學相關基礎知識、基本技能和基本思想方法的掌握程度， 考查考生的基本數學能力。

一、考核目標與要求

(一)知識要求

高等數學知識是指自治區高職院校高等數學課程標準基礎 模塊必修內容和職業模塊限定選修內容中的數學概念、性質、法 則、公式、公理、定理，以及由這些內容反映的數學思想方法， 也包括按照一定程序與步驟進行運算、分析、解決問題等基本技能。

對高等數學知識的要求依次是了解、理解、掌握三個層次。 1. 了解是指初步知道知識的含義及其簡單應用。

2.理解是指正確認識知識的概念和規律(定義、定理、法則 等)以及其它相關的聯系。

3.掌握是指在理解知識的基礎上， 能夠進行數學運算和應用 數學知識的概念、定義、定理、法則去解決實際問題。

(二) 技能與能力要求

通過高等數學的學習，學生應具備一定的數學技能與能力， 包括： 數學運算技能， 邏輯推理能力， 直觀想象能力， 數學應用 能力。(因考試不使用計算器和計算機， 故上述技能不涉及到計 算工具的使用)。各項技能和能力具體要求如下。

1.數學運算技能： 能夠根據概念、公式、法則， 或按照一定 的操作步驟，正確地進行運算求解。

2.邏輯推理能力： 能夠對問題或數學材料進行觀察、比較、 分析、綜合、抽象與概括；會用演繹、歸納和類比等進行判斷與 推理；能運用數學形式準確、清晰、有條理地進行表述。

3.直觀想象能力： 能根據條件作出正確的圖形， 根據圖形想 象出直觀形象； 能正確地分析圖形的基本元素及其相互關系； 會 運用圖形形象地提示問題的本質。

4.數學應用能力： 能閱讀、理解陳述的材料， 提煉現實問題 中各種對象的數量關系， 將現實問題轉化為數學問題， 構造數學 模型，并綜合應用所學數學知識、思想和方法加以解決。

二、考試內容與要求        

1.函數、極限與連續 ( 25 分)

( 1 )理解函數的概念，掌握簡單函數的定義域、值域的求 法和函數的表示法。

( 2 ) 掌握函數的有界性、單調性、奇偶性、周期性。

( 3 ) 了解反函數概念及其圖形性質。

( 4 ) 理解復合函數的概念。

(5)理解基本初等函數和初等函數的概念，掌握基本初等 函數的性質及其圖形。

( 6 ) 了解極限的概念及函數極限存在的條件。

( 7 ) 掌握極限的四則運算法則。

( 8 ) 掌握兩個重要極限：

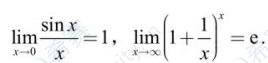
( 9 ) 理解無窮小的概念和性質， 了解無窮大與無窮小之間 的關系。

( 10)掌握無窮小階的比較方法， 會用無窮小的性質、等價 無窮小代換等方法求極限。

( 11 )了解函數極限與無窮小量的關系。

( 12)理解函數連續性的概念； 了解函數間斷點的分類， 會 判斷函數的間斷點。

( 13) 理解連續函數的和、差、積、商及復合的連續性，掌握初等函數的連續性。

( 14 )掌握閉區間上連續函數的性質及應用。 

2.一元函數導數與微分 ( 25 分)

( 1 ) 理解導數的定義，理解函數可導與連續的關系。

( 2 )理解導數的幾何意義，掌握平面曲線的切線和法線方 程的求法。

( 3)掌握基本初等函數的導數公式、導數的四則運算法則 及復合函數的求導法則。

( 4 )掌握隱函數求導法、由參數方程所確定的函數求導法。

( 5 )理解反函數的求導法則、對數求導法，了解初等函數 的求導問題。

(6)理解高階導數的定義，掌握顯函數的二階導數的計算 方法。

( 7 )理解微分的定義，掌握微分的基本公式、運算法則及 一階微分形式不變性。

3.一元函數導數的應用 ( 25 分)

( 1 ) 理解微分中值定理——羅爾定理、拉格朗日定理。

( 2 ) 掌握羅必塔法則。

( 3 ) 掌握函數單調性的判定方法。

(4) 理解函數極值的概念，并掌握其求法。

( 5 ) 掌握函數最值的求法，會求簡單的應用問題。

( 6 ) 理解曲線的凹凸性和拐點的含義，并掌握其求法。

( 7 ) 了解函數作圖的主要步驟。

4.一元函數積分學 ( 25 分)

( 1 )理解原函數與不定積分的概念，理解不定積分的基本性質。

( 2 ) 掌握不定積分的基本積分公式。

( 3)掌握不定積分的直接積分法、換元積分法與分部積分 法。

( 4 ) 理解定積分的概念及其性質。

( 5 ) 理解積分變上限函數及其求導定理。

(6) 理解并掌握牛頓——萊布尼茲公式。

( 7 )掌握定積分的直接積分法、換元積分法和分部積分法。

( 8 )了解無窮限廣義積分的概念，會求簡單的無窮限廣義 積分。

( 9 ) 掌握定積分在幾何及簡單實際問題中的應用。

三、考試形式與參考題型

(一)考試形式

考試采用閉卷、筆試形式。考試時間為 120 分鐘， 全卷滿分 100 分。考試不使用計算器。

(二)參考題型

考試題型包括單項選擇題、填空題、計算題、應用題等， 也 可以采用其它符合數學學科性質和考試要求的題型。

四、參考書目

含有上述考試內容的 《高等數學》等相關參考書目。