?全國2011年4月高等教育自學考試《高等數學(一)》試題

本試卷總分100分，考試時間150分鐘。

一、單項選擇題（每小題2分，共10分）

1.設函數f(x)=lg₂x,則f(x) + f(y)= (      )

A.f(y/x)
B.f(x-y)
C.f(x+y)
D.f(xy)

3.曲線的漸近線的條數是(      )

A.0
B.1
C.2
D.3

2.設函數,則下列結論正確的是(      )

A.f ’(0)=-1
B.f ’(0)=0
C.f ’(0)=1
D.f ’(0)不存在

4.已知f(x)是2^x的一個原函數,且f(0)=,則f(x)=(      )

A.
B.
C.
D.

5.設二元函數,則(      )

A.0
B.1
C.2
D.3

二、填空題（每小題3分，共30分）

1.函數的定義域是_________.

4.函數f(x)=2 x^3-3 x^2-12x+2的單調減少區間是_________.

5.某廠生產某種產品x個單位時的總成本函數為C(x)=100+x+x^2,則在x=10時的邊際成本為_________.

6.曲線的拐點是 _________.

10.設二元函數z=sinxy,則全微分dz=_________.

3.設函數y=xsinx^2,則_________.

7.不定積分_________.

2.函數f(x)=ln(x^2-2x+1)的間斷點的個數為_________.

8.已知,則a_________.

9.設函數,則f ’(2)=_________.

三、計算題（一）（每小題5分，共25分）

1.試確定常數a的值,使得函數在點x=0處連續.

2.求曲線y=e^x+xcos3x在點(0,1)處的切線方程.

3.求極限.

4.求微分方程滿足初始條件y|x=1=4的特解.

5.設,試比較I1與I2的大小.

四、計算題（二）（每小題7分，共21分）

1.設函數f(x)=xarcsin2x,求二階導數f”(0).

3.計算二重積分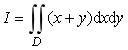,其中積分區域D是由曲線x^2+y^2=1與x軸所圍的下半圓.

2.求曲線y=3-x^2與直線y=2x所圍區域的面積A.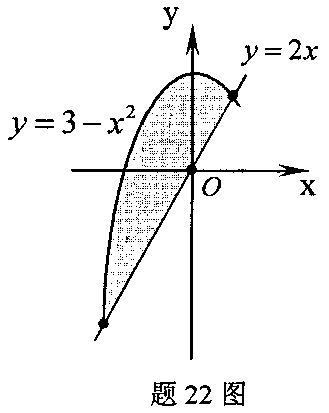

五、應用題（本題9分）

1.設某廠某產品的需求函數為Q=116-2P,其中P(萬元)為每噸產品的銷售價格,Q(噸)為需求量.若生產該產品的固定成本為100(萬元),且每多生產一噸產品,成本增加2(萬元).在產銷平衡的情況下 (1)求收益R與銷售價格P的函數關系R(P); (2)求成本C與銷售價格P的函數關系C(P); (3)試問如何定價,才能使工廠獲得的利潤最大?最大利潤是多少?

六、證明題（本題5分）

1.設函數,證明.