?全國2005年7月高等教育自學考試《高等數學（工本）》試題

點擊查看>>>全國自考00023高等數學(工本)專業歷年真題

本試卷總分100分，考試時間150分鐘。

一、單項選擇題（每小題2分，共40分）

1.不在－2的2鄰區內的點是（　　　）

A.－3
B.－1
C.－1/2
D.0

3.已知當x→0時，e^x－（ax^2+bx+1）是比x^2高階的無窮小量，則常數a, b滿足（　　　）

A.a=1, b=1
B.a=－1, b=－1
C.a=1/2, b=1
D.a=-1/2, b=-1

6.設函數y=y(x)是由方程xy^2－y+1＝0所確定的，則＝（　　　）

A.－1
B.0
C.1
D.2

9.設函數F(x)=，則F′(x)=（　　　）

A.
B.
C.
D.

11.設函數f(x)在區間［－3，－1］上連續且平均值為6，則（　　　）

A.1/2
B.2
C.12
D.18

12.點（0，1，2）到平面x－2y+2z－6=0的距離為（　　　）

A.4/3
B.0
C.2/3
D.4

14.若函數f(x,y)在(x0, y0)的某鄰域內有定義，并且存在，則f(x,y)在(x0，y0)處 （　　　）

A.連續
B.不一定連續
C.可微
D.間斷

17.在下列函數組中，線性無關的是（　　　）

A.
B.
C.
D.

19.無窮級數（　　　）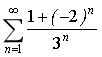

A.絕對收斂
B.條件收斂
C.發散
D.斂散性不確定

20.冪級數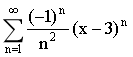的收斂區間為（　　　）

A.（2，4）
B.［2，4］
C.（2，4］
D.［2，4）

5.設函數f(x)=|x|，則f′(0)（　　　）

A.等于0
B.等于1
C.等于－1
D.不存在

8.設，則f(x)=（　　　）

A.
B.
C.
D.

13.設有直線L：及平面P：2x－3y＋z－6=0，則直線L（　　　）

A.在平面P內
B.與平面P垂直
C.與平面P平行，但不在平面P內
D.與平面P相交，但不垂直于平面P

2.極限（　　　）

A.0
B.1
C.1/2
D.∞

16.已知區域G是由坐標面和平面x+2y+z=1所圍成，則三重積分（　　　）

A.
B.
C.
D.

4.曲線（　　　）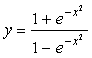

A.沒有漸近線
B.僅有水平漸近線
C.僅有垂直漸近線
D.既有水平漸近線又有垂直漸近線

15.設函數u=x^(yz)，則du|(1,1,1)＝（　　　）

A.dx
B.dx+dy+dz
C.－dx+dy+dz
D.dy+dz

10.下列廣義積分中收斂的是（　　　）

A.
B.
C.
D.

18.微分方程y″+y=0的解是（　　　）

A.y=1
B.y=x
C.y=sinx
D.y=e^x

7.已知函數f(x)在x0的某鄰區內二階可導，并且f′(x0)=0，f″(x0)<0，則（　　　）

A.（x0，f(x0)）是函數f(x)的極值點
B.（x0，f(x0)）是曲線y=f(x)的拐點
C.x0是函數f(x)的極小值點
D.f(x0)是函數f(x)的極大值

二、填空題（每小題2分，共20分）

1.函數的反函數為_______________.

6._______________.

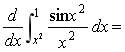2.極限＝_______________.

9.冪級數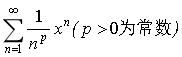的收斂半徑是_______________.

3.曲線y=e^(－x)的水平漸近線是_______________.

10.函數f(x)＝的x的冪級數展開式為_______________.

4.設函數f(x)=(x－1)(x－2)…(x－100)，則f′(1)= _______________.

5.不定積分_______________.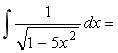

7.在空間直角坐標系中，點（1，－2，3）關于yoz坐標面的對稱點為_______________.

8.設函數z=3^xcos3y，則dz=_______________.

三、計算題（每小題5分，共25分）

1.求極限

3.設函數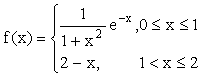，求定積分.

2.求曲線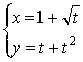　在點P（2，2）處的切線方程。

4.計算曲線積分 其中C是由A（1，1）到B（2，2）的直線段.

5.求微分方程 的通解.

四、應用和證明題（每小題5分，共15分）

1.在橢圓內作內接矩形，試問其長、寬各為多少時，矩形面積最大？此時面積值等于多少？

3.已知函數u=f(x+ay)+g(x－ay)，其中f和g均為二階可導函數，  證明：.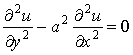

2.設函數f(x)在（－∞，＋∞）內可導，求證：若f(x)為奇函數，則f′(x)為偶函數.