?全國2005年4月高等教育自學考試《高等數學(工專)》試題

本試卷總分100分，考試時間150分鐘。

一、單項選擇題( 1—20每小題1分，21—30每小題2分，共40分)

1.函數f(x)=arccos的定義域是(      )

A.（-1，1）
B.[0，1/2]
C.（0，1）
D.（0，1/2）

2.函數f(x)=是(      )

A.奇函數
B.偶函數
C.有界函數
D.單調增函數

8.曲線y=(      )

A.的漸近線為x=0
B.的拐點為x=0
C.沒有拐點
D.的拐點為（0，0）

3.(      )

A.∞
B.1
C.0
D.不存在

6.設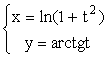 ,  則(      )

A.1/（2t）
B.1
C.2t
D.1/2

9.曲線y=x^2+的垂直漸近線是(      )

A.y=0
B.x=0
C.y=1
D.x=1

12.廣義積分(      )

A.發散
B.收斂
C.收斂于π
D.收斂于π/2

14.設z=e^xsin(x+y), 則dz|(0,π)=(      )

A.-dx+dy
B.dx-dy
C.-dx-dy
D.dx+dy

19.(      )

A.8
B.9
C.10
D.+∞

18.微分方程y"+4y'+4y=0的通解為(      )

A.
B.
C.
D.

22.設f(x)=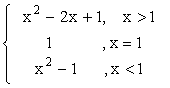 則x=1為f(x)的(      )

A.連續點
B.可去間斷點
C.無窮間斷點
D.跳躍間斷點

24.設y=sinx，則y^(10)(0)=(      )

A.-1
B.0
C.1
D.2

26.(      )

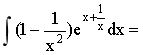A.
B.
C.
D.

27.設，則(      )

A.
B.
C.
D.

28.單葉雙曲面x^2+y^2-z^2=1與平面x=2的截線是(      )

A.圓
B.拋物線
C.一對相交相線
D.雙曲線

29.用待定系數法求微分方程y"-y'=x+3的特解時，應設特解為(      )

A.
B.
C.
D.

30.(      )

A.3/10
B.4/5
C.5/6
D.3/2

4.曲線y=在點（）處的切線的斜率為(      )

A.-4
B.-1/4
C.1/4
D.4

10.若，則f(x)=(      )

A.
B.
C.
D.

15.設函數f(x,y)=ln(1+x^2+y^2), 則f(x,y)在點（0，0）(      )

A.取得最大值0
B.取得最小值0
C.不取得極值
D.無法判斷是否取得極值

20.級數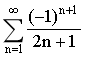是(      )

A.收斂的
B.發散的
C.絕對收斂的
D.部分和無界的級數

21.函數，則(      )

A.
B.
C.
D.

23.設C為任意常數，則e^(3x-2)dx=(      )

A.
B.
C.
D.

7.設函數f(x)在點x0處具有二階導數且f'(x0)=0，那末當f"（x0）＜0時(      )

A.函數f(x)在點x0處取得最小值
B.函數f(x)在點x0處不取得極值
C.函數f(x)在點x0處取得極大值
D.函數f(x)在點x0處取得極小值

11.=(      )

A.
B.
C.
D.

16.設區域（σ）為：(x-1)^2+y^2≤1, 則(      )

A.π
B.π/2
C.2π
D.4π

25.(      )

A.0
B.1
C.∞
D.不存在

5.設y=ln(secx+tgx), 則dy=(      )

A.
B.
C.
D.

13.過點（1，1，-1）且與平面x+2y-3z+2=0垂直的直線方程為(     )

A.
B.
C.
D.

17.四階行列式|aij|所表示的代數和中共有（      ）

A.1項
B.4項
C.16項
D.24項

二、計算題(每小題6分，共42分)

1.求

3.求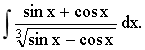

4.判定級數的斂散性.

6.計算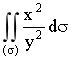，其中區域（σ）由y=x，x=2，xy=1所圍成.

7.求微分方程的通解.

2.設，討論f(x)在x=0的可導性.

5.已知函數z=e^u sinv，且u=x+y,v=xy^2，求和.

三、應用和證明題(每小題6分，共18分)

1.計算函數y=2xe^-x在[0，2]上的平均值.

3.證明：當x>0時，不等式x>ln(1+x) 成立.

2.計算由橢圓所圍成的圖形繞x軸旋轉而成的旋轉體的體積.