?自考2017年10月經管類專業線性代數考試真題

全國2017年10月高等教育自學考試線性代數(經管類)試題，課程代碼：04184

請考生按規定用筆將所有試題的答案涂、寫在答題紙上。

說明：在本卷中，AT表示矩陣A的轉置矩陣，A*表示矩陣4的伴隨矩陣，E是單位矩陣，|A|表示方陣A的行列式，r(A)表示矩陣A的秩。

選擇題部分注意事項：

1.答題前，考生務必將自己的考試課程名稱、姓名、準考證號用黑色字跡的簽字筆或鋼筆填寫在答題紙規定的位置上。

2.每小題選出答案后，用2B鉛筆把答題紙上對應題目的答案標號涂黑。如需改動，用橡皮擦干凈后，再選涂其他答案標號。不能答在試題卷上。

一、單項選擇題：本大題共5小題，每小題2分，共10分。在每小題列出的備選項中只有一項是最符合題目要求的，請將其選出。

1.設A,B是n階可逆矩陣，下列等式中正確的是

A. (A+B)-1 =A-1 +B-l B.(AB)-1=A-1B-1

C. (A-B)-1 =A-l-B-1 D. (AB)-1=B-1A-1

2.設A為3階矩陣且r(A)=l,B=

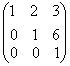
,則r(BA)=

A. 0 B. 1 C. 2 D. 3

3.設向量組α1=(1,2,3)，α2=(0,l,2)，α3=(0,0,l)，β=(1,3,6)，則

A. α1,α2,α3,β線性無關

B. β不能由α1,α2,α3線性表示

C. β可由α1,α2,α3線性表示，且表示法惟一

D. β可由α1,α2,α3線性表示，但表示法不惟一

4.設A為4×5矩陣且r(A)=4,則齊次線性方程組Ax=0的基礎解系中所含向量的個數為

A. 1 B. 2 C. 3 D. 4

5.設3階矩陣A的特征多項式為|λE-A|=(λ-2)(λ+3)2,則|A+E| =

A. -18 B. -12 C. 12 D. 18

非選擇題部分

注意事項：用黑色字跡的簽字筆或鋼筆將答案寫在答題紙上，不能答在試題卷上。

二、填空題：本大題共10小題，每小題2分，共20分。

6.行列式

的值為________.

7.設A為3階矩陣，|A|=1,則|-2A|=________.

8.設n階矩陣A的所有元素都是1,則r(A)=________.

9.設A為3階矩陣，將A的第1行與第2行交換得到矩陣B,則|A-B|=________.

10.設 3 維向量α=(3,-1,2)T，β=(3,1,4)T ,若向量γ滿足2α+γ=3β ,則γ=________.

11.已知線性方程組

無解，則數α=________.

12.設向量α=(1,1,3)，β=(1,-1,1)，矩陣A=αTβ，則矩陣A的非零特征值為________.

13.已知3階矩陣A的特征值為1,2,3,且矩陣B與A相似，則|B2+E|=________.

14.已知向量組α1=(l,2,3)，α2=(2,2,k)正交，則數k=________.

15.已知3階實對稱矩陣A的特征多項式|λE-A| =(λ-l)(λ+2)(λ-5)，則二次型?(x1,x2,x3)=xTAx的正慣性指數為________.

三、計算題：本大題共7小題，每小題9分，共63分。

16.計算4階行列式

的值。

17.已知矩陣A=(2,1,0)，B=(1,2,3)，?(x)= x2-5x + 1,求ATB及?(ATB)。

18.已知矩陣A,B滿足AX=B,其中A=

,B=

,求X.

19.求向量組α1=(1,1,1,0)T,α2=(-1,-3,5,4)T,α3=(2,1,-2,-2)T,α4=(-1,-5,11,8)的一個極大線性無關組，并將向量組中的其余向量用該極大線性無關組線性表出。

20.設3元齊次線性方程組

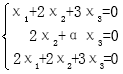
,確定α為何值時，方程組有非零解，并求其通解。

21.設矩陣A=

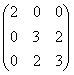
,求可逆矩陣P和對角矩陣Λ，使得P-1AP=Λ。

22.已知?(x1,x2,x3)=x12+4x22+2x32+2tx1x2-2x1x3為正定二次型，(1)確定t的取值范圍;(2)寫出二次型?(x1,x2,x3)的規范形。

四、證明題：本題7分。

23.證明矩陣A=

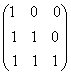
不能對角化。