?江西2022年專升本高等數學及其應用考試大綱

江西2022年專升本高等數學及其應用考試大綱

Ⅰ.考試內容與要求

本科目考試內容包括函數、極限、連續、一元函數微分學及其應用、 一元函數積分學及其應用、多元函數微分學及其應用、二重積分及其應用、 常微分方程等。主要考查考生對基本概念和基本理論的理解，運用基本理 論和基本方法進行計算的能力，以及綜合運用所學知識分析并解決簡單的 實際問題的能力。對考試內容的要求由低到高，概念和理論的要求分為 “了解”和“理解”兩個層次; 方法和運算的要求分為“掌握”和“熟練 掌握”兩個層次。具體內容與要求如下。

一、函數、極限和連續

(一) 函數

1.理解函數的概念，掌握函數(含分段函數) 的定義域、表達式及函 數值的求法，掌握實際問題的函數關系式的建立。

2.了解函數的單調性、奇偶性、有界性和周期性的概念。 3.了解反函數的概念。

4.掌握函數的四則運算與復合運算，熟練掌握復合函數的復合過程。 5.熟練掌握基本初等函數的性質及其圖象。 6.了解初等函數的概念。

(二) 極限

1.了解數列極限的概念。

2.了解函數極限的概念，理解函數極限存在的充分必要條件。

3.熟練掌握極限的四則運算法則。

4.熟練掌握兩個重要極限。

5.了解無窮小量、無窮大量的概念、無窮小量的性質、無窮小量與無 窮大量的關系。理解高階、低階、同階和等價無窮小量的概念,熟練掌握

等價無窮小代換求極限的方法。

(三) 連續

1.理解函數在一點連續與間斷的概念，掌握函數(含分段函數) 連續 性的判斷方法。

2.掌握求函數的間斷點并判斷其類型的方法。

3.了解閉區間上連續函數的最值定理、介值定理、零值定理。

4.理解初等函數在其定義區間上的連續性，掌握用函數連續性求極限 的方法。

二、一元函數微分學及其應用

(一) 導數與微分

1.理解導數的概念、導數的幾何意義、函數可導性與連續性之間的關

系，掌握用導數定義判斷函數在一點處的可導性的方法。

2.掌握曲線的切線方程與法線方程的求法。 3.熟練掌握導數的基本公式、四則運算法則、復合函數的求導法則。 4.掌握隱函數和由參數方程所確定的函數的求導法，掌握對數求導法。 5.理解高階導數的概念，掌握高階導數的求法。

6.理解函數微分的概念，理解可微與可導的關系、微分的四則運算法 則、一階微分的形式不變性，掌握函數微分的求法。

(二) 微分中值定理與導數的應用

1.了解羅爾中值定理、拉格朗日中值定理。

2.熟練掌握用洛必達法則求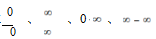型未定式的極限。

3.掌握用導數判定函數單調性的方法，掌握函數的單調區間的求法。

4.了解函數極值的概念，掌握函數的極值和最值的求法，熟練掌握實 際問題最值的求法。

5.掌握曲線凹向的判定方法，掌握曲線的凹凸區間和拐點的求法。

三、一元函數積分學及其應用

(一) 不定積分

1.理解原函數與不定積分的概念，掌握不定積分的性質。 2.熟練掌握基本積分公式。 3.熟練掌握不定積分第一換元法，掌握不定積分第二換元法。 4.熟練掌握不定積分的分部積分法。

(二) 定積分

1.了解定積分的概念，理解定積分的幾何意義，了解函數可積的條件。 2.掌握定積分的基本性質。

3.理解變限積分函數的概念，熟練掌握變上限函數的導數。 4.熟練掌握牛頓-萊布尼茨公式。 5.熟練掌握定積分的換元積分法與分部積分法。

(三) 定積分的應用

1.熟練掌握直角坐標系下用定積分計算平面圖形面積的方法。 2.掌握求平面圖形繞坐標軸旋轉所生成的旋轉體體積的方法。

四、常微分方程

(一) 一階微分方程

1.了解微分方程的基本概念。

2.熟練掌握可分離變量微分方程的解法。

3.掌握齊次微分方程的解法。

4.掌握一階線性微分方程的解法。

(二) 二階線性微分方程

1.了解二階線性微分方程解的結構。

2.掌握二階常系數齊次線性微分方程的解法。

五、多元函數微分學及其應用

(一) 多元函數微分學

1.了解多元函數的概念、二元函數的幾何意義、二元函數的極限與連 續的概念，掌握二元函數定義域的求法。

2.理解偏導數的概念，熟練掌握多元函數一、二階偏導數的求法。

3.了解全微分的概念，理解全微分存在的必要條件與充分條件，掌握 多元函數全微分的求法。

4.掌握多元復合函數的求導法則。

5. 了解隱函數存在定理 ，掌握求由方程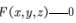所確定隱函數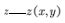的一階偏導數的方法。

6.掌握求二元函數極值的方法。

(二) 多元函數微分學的應用

1.掌握求解實際問題中的多元函數最值的方法。

2.掌握用拉格朗日乘數法求解實際問題最值的方法。

六、二重積分及其應用

1.了解二重積分的概念與性質，理解二重積分的幾何意義。

2.熟練掌握二重積分在直角坐標系和極坐標系下的計算方法，掌握交 換二次積分的積分次序的方法。

3.掌握用二重積分計算空間立體體積的方法。

Ⅱ.考試形式與題型

一、考試形式

考試采用閉卷、筆試形式，試卷滿分 150 分，考試時間 120 分鐘。

二、考試題型

考試題型從以下類型中選擇： 單項選擇題、填空題、計算題、解答題、

應用題等。

Ⅲ.參考書目

1.“十三五”職業教育國家規劃教材： 凌巍煒，謝良金.高等數學(基 礎模塊) .東北師范大學出版社，2020.03. ISBN:978-7-5681-3496-5.

2.“十三五”職業教育國家規劃教材：高等數學(第五版) . 高等教育出版社,2018.09. ISBN:978-7-04-050385-2.