?福建2022年專升本高等數學考試大綱

福建2022年專升本高等數學考試大綱

一、考試范圍

第一章 函數、極限與連續

第二章 導數與微分

第三章 微分學及應用

第四章 一元函數積分學

第五章 空間解析幾何

第八章 常微分方程

第一章 函數、極阻與連續

(一)考核知識點

1、一元函數的定義。

2、函數的表示法(包括分段表示法)。

3、函數的簡單性——有界性、單調性、奇偶性、周期性。

4、反函數及其圖形。

5、復合函數。

6、基本初等函數與初等函數(包括它們的定義、定義區間、簡單性態和圖形)。

7、數列概念。

8、數列的極限。

9、收斂數列的性質——有界性、唯一性。

10、數列極限的存在準則——單調有界準則。

11、函數的極限(包括當和時，函數極限的定義及左、右極限的定義)。

12、函數極限的存在。

13、函數極限的存在準則——夾逼準則。

14、極限的四則運算法則(包括數列極限與函數極限)。

15、兩個重要極限：

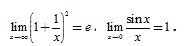
16、無窮小量的概念及其運算性質。

17、無窮小量的比較。

18、無窮大量及其與無窮小量的關系。

19、函數極限與無窮小量的關系。

20、函數的連續性。

21、函數的間斷點。

22、連續函數的和、差、積、商及復合的連續性。

23、初等函數的連續性。

24、閉區間上連續函數的性質。

(二)考試要求

函數是數學中最重要的基本概念之一，它是客觀世界中量與量之間的依存關系在數學中的反映，也是高等數學的主要研究對象。極限理論是高等數學的基石，函數連續性的概念就在它的基礎上建立起來的，極限也是研究導數、積分、級數等必不可少的基本概念和工具。

本章總的要求是：深刻理解一元函數的定義;掌握函數的表示法和函數的簡單性態;理解反函數概念和復合函數概念;熟練掌握基本初等函數和了解什么是初等函數。深刻理解極限概念;了解極限的兩個存在準則——單調有界準則和夾逼準則;熟練掌握極限的四則運算法則;牢固掌握兩個重要極限;理解無窮小量，掌握它的性質;掌握無窮小量的比較;理解無窮大量及其與無窮小量的關系;理解極限與無窮小量的關系;理解函數連續性的概念;了解函數的間斷點;熟練掌握連續函數的性質;掌握初等函數的連續性及閉區間上連續函數的性質。

本章考試的重點是：函數的定義;基本初等函數;極限概念與極限運算;無窮小的比較;連續概念與初等函數的連續性。

第二章 導數與微分

(一)考核知識點

1、導數的定義。

2、導數的幾何意義。

3、導數作為函數對自變量的變化率的概念。

4、平面曲線的切線與法線。

5、函數可導與連續的關系。

6、可導函數的和、差、積、商的求導運算法則。

7、復合函數的求導法則。

8、反函數的求導法則。

9、基本初等函數的求導公式及初等函數的求導問題。

10、高階導數。

11、隱函數求導和取對數求導法。

12、由參數方程所確定的函數的求導法。

13、微分的定義。

14、微分的基本公式、運算法則和一階微分形式不變法。

(二)考試要求

導數概念是根據解決實際問題的需要，在前一章函數與極限這兩個概念的基礎上建立起來的，它是微分學中最重要的概念。微分概念是微分學中又一個重要概念，它與導數有著密切的聯系。兩者在科學技術與工程實際中有著廣泛的應用。

本章總的要求是：深刻理解導數的定義，了解它的幾何意義和它作為變化率的概念;掌握平面曲線的切線方程和法線方程的求法;理解函數可導與連續的關系;熟練掌握函數和、差、積、商求導的運算法則、復合函數求導法則、反函數求導法則;熟練掌握基本初等函數的求導公式和了解初等函數的求導問題;掌握隱函數求導法、取對數求導法、由參數方程所確定的函數求導法;理解高階導數的定義;熟練掌握微分的運算法則及一階微分形式不變性。

本章考試的重點是：導數的定義及其幾何意義;導數作為變化率的概念;可導函數的和、差、積、商的求導運算法則;復合函數求導法則;初等函數的求導問題;微分定義。

第三章 微分學應用

(一)考核知識點

1、微分中值定理——羅爾定理、拉格朗日定理、柯西定理。

2、羅必塔法則。

3、函數增減性的判定。

4、函數的極值及其求法。

5、函數的最大、最小值及其應用問題。

6、曲線的凹向及其判定法。

7、拐點及其求法。

8、函數作圖。

9、弧微分。

(二)考試要求

微分學應用以導數為主要工具，結合諸如函數、極限、連續等概念，綜合地用來對函數進行較全面的研究以及解決一些較簡單的實際問題。微分學應用的理論基礎是微分中值定理。

本章總的要求是：深刻理解微分中值定理;熟練掌握羅必塔法則;掌握函數增減性的判定;理解函數極值的概念，并掌握其求法;理解函數最大值、最小值的意義，掌握其求法，并能解決簡單的最大、最小值應用問題;了解曲線的凹向和拐點的含義，并能掌握其求法;掌握函數作圖的主要步驟;知道弧微分概念及其計算公式。

本章考試的重點是：微分中值定理;羅必塔法則;函數增減性的判定;函數的極值及其求法;函數的最大、最小值及其應用問題。

第四章 一元函數積分法

(一)考核知識點

1、原函數的定義。

2、不定積分的定義。

3、原函數與不定積分的幾何意義。

4、不定積分的基本性質。

5、基本積分公式。

6、不定積分的分項積分法則。

7、換元積分法則。

8、分部積分法則。

9、簡單有理函數和可化為簡單有理函數的積分法。

10、定積分的定義及其存在定理。

11、定積分的基本性質——對區間的可加性、線性性質、估值不等式。

12、定積分的中值定理(包括積分均值)。

13、微積分學基本定理。

14、牛頓——萊布尼茲公式。

15、定積分的換元積分法則。

16、定積分的分部積分法則。

17、兩種廣義積分——無界函數的廣義積分及積分區間為無窮區間的廣義積分。

18、定積分的應用——幾何應用和物理應用。

(二)考試要求

與加法有逆運算減法、乘法有逆運算除法一樣，求導法也有逆運算，這就是不定積分法。與導數概念的產生一樣，定積分概念也是由解決實際問題的需要而產生的。本章內容豐富，概念性強。

本章總的要求是：深刻理解原函數與不定積分的定義;理解不定積分的基本性質;牢固掌握基本積分公式;熟練掌握并能靈活運用分項積分法則、換元積分法則與分部積分法則; 掌握簡單有理函數和可化為簡單有理函數的積分法。深刻理解定積分的定義及其存在定理;理解定積分的基本性質和定積分的中值定理;深刻理解并熟練掌握微積分學基本定理;理解并掌握牛頓——萊布尼茲公式;熟練掌握定積分的換元積分法則和分部積分法則;理解兩種廣義積分的概念并掌握它們的求法;掌握定積分在幾何和物理方面的應用。

本章考試的重點是：原函數與不定積分概念;基本積分公式;換元積分法則與分部積分法則;定積分的概念;定積分的中值定理;微積分學基本定理;牛頓——萊布尼茲公式;定積分的換元積分法則，定積分的幾何應用。

第五章 空間解析幾何

(一)考核知識點

1、空間直角坐標系、兩點之間的距離公式。

2、向量概念、方向余弦與方向數。

3、向量的運算、向量平行垂直的條件。

4、平面方程。

5、空間直線方程。

6、平面、直線間的平行垂直關系。

7、曲面與空間曲線方程。

8、二次曲面簡介。

(二)考試要求

與平面解析幾何一樣，空間解析幾何研究的兩個基本問題是：

(1)已知構成曲面和曲線的幾何條件，建立它們的方程;(2)已知曲面或曲線的方程，研究它們的圖形和特點。

本章總的要求是：理解空間直角坐標系;掌握兩點之間的距離公式、向量概念、向量的運算、向量平行垂直的條件、方向余弦與方向數。平面與空間直線的方程和它們之間的平行及垂直關系;掌握曲面與空間曲線的方程;掌握常用的幾個二次曲面的標準方程和它們的圖形。

本章考試的重點是：向量概念、向量的運算、向量平行及垂直的條件;平面的方程;直線的方程;球面方程;母線平行于坐標軸的柱面方程。

第八章 常微分方程

(一)考核知識點

1、微分方程的一般概念——微分方程的定義、階、解、通解、初始條件、特解。

2、可分離變量的微分方程。

3、齊次方程。

4、一階線性方程。

5、可降階的三種特殊類型的方程：

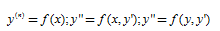
6、二階線性微分方程解的結構。

7、二階常系數齊次線性微分方程。

8、二階常系數非齊次線性微分方程。

9、用微分方程解決實際問題。

(二)考試要求

微分方程的起源與研究幾何、力學、物理等方面的問題有著密切的聯系，它的理論與方法幾乎是與微積分學同時發展起來的，微分方程有著廣泛的應用。到現代，它已經滲透到自然科學、工程技術、生物醫學等各個領域。

本章總的要求是：理解微分方程的一般概念;熟練掌握可分離變量的方程、齊次方程、一階線性方程的解法;掌握可降階三種特殊類型的微分方程的解法;深刻理解二階線性微分方程解的結構;熟練掌握二階常系數齊次與非齊次線性微分方程的解法;掌握用微分方程解決實際問題的步驟。

本章考試的重點是：微分方程的一般概念;可分離變量的微分方程;一階線性微分方程;二階常系數線性齊次微分方程的解法;二階常系數非齊次線性微分方程的特解的求法;識別微分方程的各種類型。

二、考試命題用書

《高等數學》，福建省教育廳組編，徐榮聰主編，莊興無主審，廈門大學出版社2004年8月第二版。